Objekttypen und Datentypen
Insgesamt sind folgende Objekttypen für Grafikprogrammierung relevant:
Art | Datentyp via TYPE$() - Funktion |
Punkte oder Vektoren | VECTOR |
Streckenzüge | SEGMENT |
Kreise und Kreisbögen | ARC |
Profile | LIST |
Raumpunkte | LIST |
Extrusionspfade | LIST |
Punkte oder Vektoren
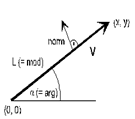
Unter einem Vektor versteht man in der analytischen Geometrie ein mathematisches Objekt, das eine Parallelverschiebung in der Ebene oder im Raum beschreibt. Solche Vektoren werden durch kartesische Koordinaten dargestellt, das sind in der Ebene Paare und im Raum Tripel von Zahlen, die oft untereinander (als Spaltenvektoren) geschrieben werden.
Im visuellen Parametersystem sind ein Punkt und ein Vektor dasselbe, d.h. ein Punkt hat auch hier die Eigenschaften Länge und Winkel, die er eigentlich nicht haben dürfte. Dies funktioniert nur deswegen, weil im visuellen Parametersystem immer der Ursprungspunkt [0,0] dabei ist und somit bei einer Definition eines Punktes immer eine Strecke ausgehend von [0,0] zu dem definierten Punkt entsteht.
Man hat folgende Möglichkeiten einen Punkt oder Vektor zu definieren:
P1 = [1,1] !Standard
P1 = VECTOR(1,1) !Selten
P1 = POINT(1,1) !Sehr selten
P1 = POLAR(SQRT(2),PI/4) !Oft praktisch
Alle Variablen die vom Typ Vector sind, besitzen automatisch folgende Attribute:
Attributname | Bedeutung |
Vector.x | X-Koordinate des Vektors |
Vector.y | Y-Koordinate des Vektors |
Vector.arg | Winkel (Argument) des Vektors |
Vector.mod | Länge des Vektors |
Vector.norm | orthonormaler Vektor des Vektors |
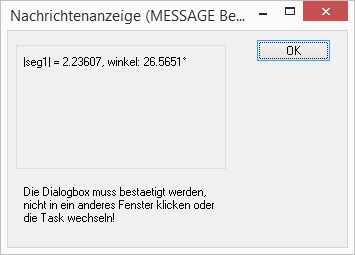
PROCEDURE VektorenBeispiel
DEFINE VARIABLE P0, P1, seg1
P0 = [0,0]
P1 = [1,1]
P2 = [2,1]
seg1 = SEGMENT(P1,P1+P2)
MESSAGE "|seg1| = " + str$(seg1.mod)+", winkel: "+ str$(deg(seg1.arg))+"°"
END
.png)
Streckenzüge
Verbindet man zwei Punkte so erhält man einen Streckenzug. Im visuellen Parametersystem erreich man das durch die Segment-Anweisung.
P1 = [1,1]
P2 = [2,1]
seg1 = SEGMENT(P1,P1+P2)
Durch eine solche Definition sind automatisch folgende Attribute verfügbar:
Attributname | Bedeutung |
Segment.v1 | Anfangsvektor (Punkt1) der Strecke |
Segment.x1 | X-Koordinate des Anfangspunkts |
Segment.y1 | Y -Koordinate des Anfangspunkts |
Segment.v2 | Endvektor (Punkt2) der Strecke |
Segment.x2 | X-Koordinate des Endpunkts |
Segment.y2 | Y -Koordinate des Endpunkts |
Segment.v | Trägervektor der Strecke |
Segment.arg | Richtungswinkel der Strecke |
Segment.mod | Länge der Strecke |
Segment.norm | orthonormaler Vektor der Strecke (nur lesen) |
Über die interne Funktion INTERSECTION() können Schnittpunkte zwischen Streckenzügen ermittelt werden. Über die interne Funktion ADJUST() kann eine Streckenzugliste geschlossen werden.
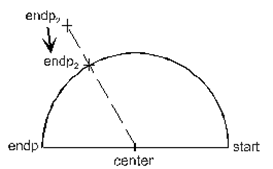
Kreise und Kreisbögen
In Profilen können Streckenzüge und Kreise und Kreisbögen verwendet werden. Ein Beispiel für ein Profil wo Streckenzüge und ein Kreisbogen vorkommen wäre ein Segmentbogenfenster.
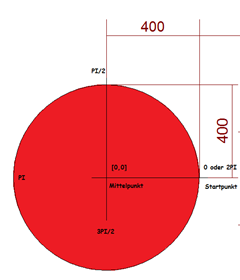
Kreisdefinition in der Makrosprache:
kreis = ARC(Mittelpunkt, StartPunkt, Winkel)
Winkel = PI/4 !8tel Kreis (45° Grad)
Winkel = PI !Halbkreis
Winkel = 2*PI !Vollständiger Kreis
Bsp.: Kreis = ARC([0,0], [400,0], 2*PI)
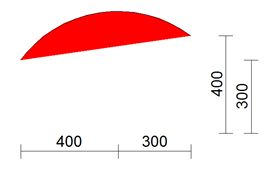
Kreisbogendefinition in der Makrosprache:
kb = ARCFROMSTRINGH(Vektor 1, Vektor 2, Sehnenhöhe)
p1 = [ 0, 0]
p2 = [700, 0]
p3 = [700, 400]
p4 = [ 0, 300]
Bogen = ARCFROMSTRINGH(p3, p4, 100)
lstSegA = {SEGMENT(p1,p2), SEGMENT(p2,p3), Bogen, SEGMENT(p4,p1)}
Kreise und Kreisbögen haben immer folgende Attribute:
Attributname | Bedeutung |
Arc.start | Anfangsvektor des Kreisbogens |
ARC.V1 | Analog zu .START |
Arc.center | Zentrumsvektor des Kreisbogens |
Arc.endp | Endvektor des Kreisbogens (wenn er verändert wird und dadurch außerhalb der Kreislinie liegt, wird nur die Bogenlänge geändert und der Endpunkt wieder auf die Kreislinie gesetzt) |
ARC.V2 | Analog zu .ENDP |
Arc.ang | Verlaufswinkel des Kreisbogens (ang > 0 bei pos. Umlaufsinn, ang < 0 bei neg. Umlaufsinn) |
Arc.r | Radius des Kreisbogens = Länge der Strecke, die center und start miteinander bilden |
Arc.length | Länge des Kreisbogens |
Arc.arg | Richtungswinkel der Strecke, die center und start miteinander bilden |
Arc.stringH | Sehnenhöhe des Kreisbogens |
Profil
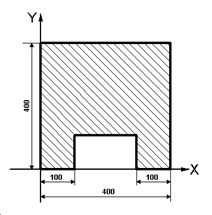
Oder auch Konturen oder englisch Outlines genannt, sind vom Datentyp Listen, die Streckenzüge, Kreisbögen oder Kreissegmente enthalten, welche geschlossen sind. Ein geschlossener Streckenzug muss immer eine Fläche enthalten, damit man eine Extrusion durchführen kann, d.h. ein Profil muss mindestens 3 Streckenzüge oder zumindest einen Kreis enthalten, damit der Streckenzug geschlossen ist.
Definition in der Makrosprache:
lstProfil = {SEGMENT(p1,p2), SEGMENT(p2,p3),…,SEGMENT(pN,p1)}
Beispiel:
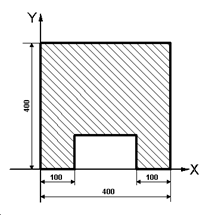
p1 = [0, 0]
p2 = [100, 0]
p3 = [100, 100]
p4 = [300, 100]
p5 = [300, 0]
p6 = [400, 0]
p7 = [400, 400]
p8 = [ 0, 400]
lstProfil = {SEGMENT(p1,p2), SEGMENT(p2,p3), SEGMENT(p3,p4), SEGMENT(p4,p5),
SEGMENT(p5,p6), SEGMENT(p6,p7), SEGMENT(p7,p8), SEGMENT(p8,p1)}
Profile können über fix definierte Funktionen wie SPLIT() geteilt oder über EXTRUDE() verkleinert bzw. vergrößert werden.
Extrusionbefehl
Aufruf
objID = 0
RUN Extrusion( objID, !ID des erzeugten Objektes
lstProfil, !Geschlossener 2D-Streckenzug
RelPK, !Relationspunkt Kontur
Referenzvektor, !Referenzvektor
lstExtrusionspfad, !Liste mit 3D-Streckenzügen
optional layer) !Layer
Parameter
objID:
Bei erfolgreichem Erstellen des Extrusionskörpers wird die dementsprechende ID des Szenarios zurückgegeben, mit welcher zu einem späteren Zeitpunkt wieder Manipulationen durchgeführt werden können. Zuvor sollte diese Variable immer auf 0 gesetzt werden!
lstProfil:
Entspricht einem geschlossenen Streckenzug. Ein Streckenzug besteht immer aus zwei Punkten in 2D. Diese Streckenzüge werden durch Segment-Anweisungen erzeugt und stehen alle in einer Liste.
lstProfil = { Segment(Punkt1, Punkt2),Segment(Punkt2, Punkt3),Segment(PunktN, Punkt1) }
RelPK:
Der Relationspunkt wo in der Kontur mit der Extrusion begonnen werden soll (Standard = [0,0]).
Der Kurvenzug ist der Extrusionspfad!
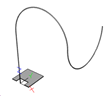
Relationspunkt auf [200,0]
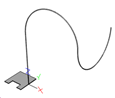
Relationspunkt auf [400,200]
Referenzvektor:
Die Drehung der 2D Figur in Bezug auf den Pfad wird durch den Referenzvektor festgelegt, in den die X Achse der 2D Figur gedreht werden soll. Diese Achsdrehung gilt für den Anfangspunkt des Pfades.
.png)
{1, 0, 0}
.png)
{1, 1, 0}
.png)
{0, 1, 0}
Gängige Referenzvektoren sind {1,0,0} für links nach rechts gerichtete Extrusionspfade (Bsp.: {{{0,0,0},{1000,0,0}}} und {0,1,0} für Extrusionspfade die von hinten nach vorne in y-Richtung gehen, z.b.: {{{0,10,0},{0,0,0}}}
Der Referenzvektor ist die Lage der x – Achse(2D) im 3D – Raum, d.h. mit {0,1,0} wird die x- Achse der 2D Outline auf die y-Achse im 3D – Raum gedreht.
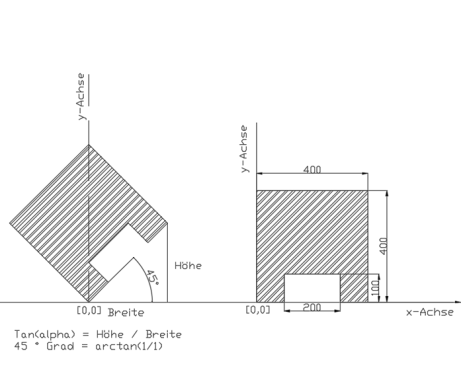
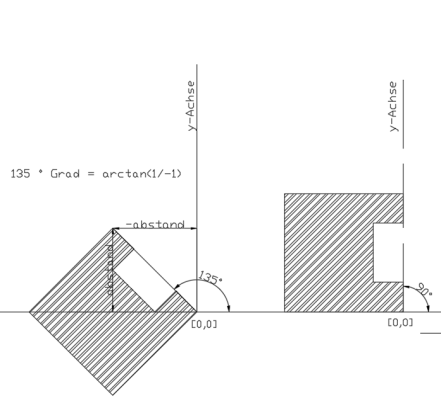
Nimmt man eine Extrusion die von unten nach oben geht, so verhalten sich folgende Referenzvektoren für die x-Achse folgendermaßen. Verwendet wird das rechts abgebildete Profil.
Referenzvektor | Drehung der x-Achse |
{ 1, 0, 0} | 0° |
{ 1, 1, 0} | 45° |
{ 0, 1, 0} | 90° |
{-1, 1, 0} | 135° |
{-1, 0, 0} | 180° |
{-1,-1, 0} | 225° |
{ 0,-1, 0} | 270° |
{ 1,-1, 0} | 315° |
Extrusionsdaten
vRelPunkt = [0,0]
P1_3D = {0, 0, 0}
P2_3D = {0, 0, 300}
lstEPath = {{P1_3D,P2_3D}} !Erste Extrusion unten

lstExtrusionspfad:
Der Extrusionspfad beschreibt den Weg anhand einer Liste voller Raumstrecken nach der das Profil extrudiert werden soll.
Aufbau eines Extrusionspfades:
Raumpunkt1 = {0, 0, 0}
Raumpunkt2 = {1000, 0, 0}
RaumpunktN = {0,0,1000}
lstPfad1_3d = {Raumpunkt1, Raumpunkt2}
lstPfad2_3d = {Raumpunkt2, Raumpunkt3}
lstPfadN_3d = {RaumpunktN, Raumpunkt1}
ExtPfad_3d = {lstPfad1_3d, lstPfad2_3d, …, lstPfadN_3d}
Programmcode Referenzvektorbeispiel
!Profil mit verschiedenen Referenzvektor zeichnen
lstReferenzVektoren = {{ 1, 0, 0},
{ 1, 1, 0},
{ 0, 1, 0},
{-1, 1, 0},
{-1, 0, 0},
{-1,-1, 0},
{ 0,-1, 0},
{ 1,-1, 0},
{ 1, 0, 0}}
i = 0
FOR i = 1 TO lstReferenzvektoren.NUM DO BEGIN
lstRefVektor = lstReferenzVektoren[i]
RUN RefVektorExtrusion_Mit_Versetzter_XAchse(i-1,nID, lstProfil,
vRelPunkt, lstRefVektor,lstEPath, 4*nS, (i-1)*nOffsetZ)
END
PROCEDURE RefVektorExtrusion_Mit_Versetzter_XAchse
DEFINE PARAMETER INPUT pnI, INPUTOUTPUT pnID, INPUT plstProfil,
INPUT pvRelPunkt, INPUT plstRefVektor,
INPUT plstEPath, INPUT pBreite, pnOffsetZ=0
DEFINE VARIABLE vektor2D, wi_rad, wi, pBem_3D1, pBem_3D2
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!Mathematische Überlegungen
!vektor2D = polar(sqrt(plstRefVektor[1]^2 + lstRefVektor[2]^2),
! ATN(plstRefVektor[2] / plstRefVektor[1]))
!Divsion durch 0 ergibt unendlich, TAN(unendlich)= PI/2 = 90° Grad
!Daher wird vektor2D wird aus dem Referenzvektor hergeleitet!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!
vektor2D = VECTOR(plstRefVektor[1], plstRefVektor[2])
wi = pnI * 45
vektor2D.MOD = pBreite
pBem_3d1 = {0, 0, pnOffsetZ}
pBem_3d2 = {vektor2D.x, vektor2D.Y, pnOffsetZ}
RUN public\lib3d.DRAWMEASURELINE(nID,pBem_3D1[1], pBem_3D1[2],
pBem_3D1[3],pBem_3D2[1], pBem_3D2[2], pBem_3D2[3],STR$(wi)+"°")
pnID = 0
RUN public\lib3d.EXTRUSION(pnID, plstProfil, pvRelPunkt, plstRefVektor, plstEPath)
RUN public\lib3d.TRANSLATEBY(pnID, 0, 0, pnOffsetZ)
RUN public\lib3d.BEAUTIFY(pnID, 30)
END